𝗙𝗹𝗼𝗮𝘁𝗶𝗻𝗴 𝗣𝗼𝗶𝗻𝘁 - máy tính liệu có tính SAI???
Đã bao giờ bạn thực hiện phép so sánh kiểu như 𝟬.𝟭 + 𝟬.𝟮 == 𝟬.𝟯 và ra kết quả 𝗙𝗮𝗹𝘀𝗲 chưa? Bạn thắc mắc "liệu máy tính có thông minh như mình nghĩ"? Thực ra đây lại là một kiến thức nền trong ngành CNTT mà đa số các trường đại học đều đề cập đến nhưng có thể bạn đã quên, hãy đọc bài viết này để biết lý do nào 😎
Thay vì trình bày khái niệm 𝗗𝗮̂́𝘂 𝗰𝗵𝗮̂́𝗺 đ𝗼̣̂𝗻𝗴 (floating point) là gì như trên wiki, cái mà mấy ông "khủng long" mới hiểu, thì chúng ta hãy bắt đầu bằng pain point, hay lý do mà dấu chấm động được ra đời nhé! Ít nhiều khi chúng ta tìm hiểu về IT và khoa học máy tính đều biết rằng dữ liệu của chúng ta được máy tính lưu dưới dạng một dãy nhị phân dạng 01011011... giải thích đơn giản cho điều này là vì phần cứng máy tính hiện nay chỉ xác định được hai trạng thái là bật - tắt (tương ứng với 0 và 1) 🤣. Để lưu một số nguyên máy tính chỉ đơn giản là chuyển đổi nó sang hệ nhị phân (binary) theo một chuẩn 8bit, 16bit, 32bit,...
Ví dụ số 𝟱 => hệ nhị phân là 𝟬𝟭𝟬𝟭, chuẩn 8bit là 𝟬𝟬𝟬𝟬 𝟬𝟭𝟬𝟭. Rất đơn giản đúng không 👌
Hmm... vậy số thực thì chỉ cần thêm một bit hoặc vị trí nào đó để xác định dấu chấm ở giữa thôi đúng không 🤔 Vậy thì với 8bit, chúng ta coi 4 bit đầu là phần nguyên, 4 bit sau là phần thập phân... 𝘖𝘩 𝘴𝘩𝘫𝘵, 𝘮𝘪𝘴𝘴𝘪𝘰𝘯 𝘤𝘰𝘮𝘱𝘭𝘦𝘵𝘦𝘥 😎
Wait a minute, 8 bit sẽ biểu diễn tối đa được giá trị trong khoảng [𝟬 - 𝟮𝟱𝟱] (để đơn giản hóa mình sẽ bỏ phần dấu âm/dương), như vậy nếu chúng ta chia đôi số bit thành 4/4 để biểu diễn số thực thì sẽ ra sao? Liệu có phải một phát minh vĩ đại? Nhưng không, ta chỉ có thể biểu diễn được từ [𝟬.𝟬 - 𝟭𝟱.𝟵𝟯𝟳𝟱]... 𝘖𝘩 𝘴𝘩𝘫𝘵, 𝘩𝘦𝘳𝘦 𝘸𝘦 𝘨𝘰 𝘢𝘨𝘪𝘢𝘯!
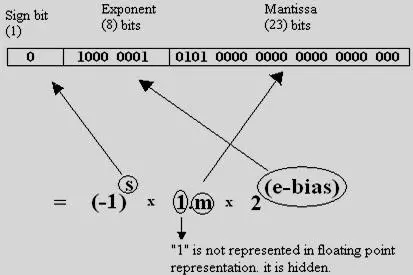
Vậy 𝗳𝗹𝗼𝗮𝘁𝗶𝗻𝗴 𝗽𝗼𝗶𝗻𝘁 đã làm gì để vừa biểu diễn được số thực, vừa tiết kiệm được không gian lưu trữ? Giải pháp cho vấn đề này, 𝗳𝗹𝗼𝗮𝘁𝗶𝗻𝗴 𝗽𝗼𝗶𝗻𝘁 không sử dụng hoàn toàn số bit để lưu giá trị của số, thay vào đó nó chia ra thành 3 thành phần (theo chuẩn IEEE 32bit) như sau:
- 𝙎𝙞𝙜𝙣 [1bit]: biểu diễn dấu "-" hoặc "+". Giá trị tương ứng 0 là số dương, còn 1 là số âm (đừng nhầm lẫn nhé)
- 𝗘𝘅𝗽𝗼𝗻𝗲𝗻𝘁 [8bit]: xác định vị trí của dấu chấm động, là thứ "hay ho" nhất
- 𝙈𝙖𝙣𝙩𝙞𝙨𝙨𝙖 [23bit]: chính là giá trị của số sau khi đã dịch chuyển dấu chấm.
=> Máy tính sẽ đọc một số thực với format: <𝙎𝙞𝙜𝙣+𝗘𝘅𝗽𝗼𝗻𝗲𝗻𝘁+𝙈𝙖𝙣𝙩𝙞𝙨𝙨𝙖>
Cùng xem nó hoạt động rao sao nào 🥸
Cơ chế của dấu chấm động chính là "linh động" dấu chấm thập phân, cho phép dịch chuyển dấu chấm thập phân đến bất kì vị trí nào, điều này thực sự làm nên sức mạnh rất to lớn, thử 1 ví dụ đơn giản nhé:
Quay lại ý tưởng chia 4/4 của 8bit bên trên để lưu số thập phân, phần nguyên lớn nhất ta biểu diễn được là 𝟭𝟱, vậy muốn biểu diễn 𝟭𝟲 thì phải làm thế nào?
👉 𝟭𝟲 = 𝟭𝟲.𝟬, tương đương với 𝟭.𝟲𝟬 * 𝟭𝟬^𝟭
Như bạn thấy, chúng ta đã dịch chuyển dấu chấm sang bên trái 1 cấp, phần nguyên của ta chỉ còn 𝟭, phần thập phân là 𝟬.𝟲, vậy là chúng ta đã có thể biểu diễn phần nguyên 𝟭𝟲 theo chuẩn 8bit, nhưng với điều kiện là chúng ta phải nhân thêm với 𝟭𝟬^𝟭.
Nói một cách đơn giản dễ hiểu 𝟭.𝟲𝟬 chính là 𝙈𝙖𝙣𝙩𝙞𝙨𝙨𝙖, ^𝟭 chính là 𝗘𝘅𝗽𝗼𝗻𝗲𝗻𝘁, còn 𝙎𝙞𝙜𝙣 sẽ mang giá trị 𝟬 vì đây là số dương. Máy tính sử sử dụng 3 giá trị trên để hiểu được giá trị số thực được lưu. Tuy vậy, thực tế sẽ phức tạp hơn một chút khi máy tính cần phải chuyển đổi hệ số theo các chuẩn lưu trữ (nếu các bạn muốn mình sẽ làm thêm một bài hướng dẫn chuẩn hóa số thực áp dụng floating point bằng tay nhé).
Một ví dụ thực tế hơn: 𝟬.𝟭 => 𝟬 𝟬𝟭𝟭𝟭𝟭𝟬𝟭𝟭 𝟭𝟬𝟬𝟭𝟭𝟬𝟬𝟭𝟭𝟬𝟬𝟭𝟭𝟬𝟬𝟭𝟭𝟬𝟬𝟭𝟭𝟬𝟭
Quay lại vấn đề ban đầu: 𝟬.𝟭 + 𝟬.𝟮 = 𝟬.𝟯𝟬𝟬𝟬...𝟬𝟰, vậy liệu máy tính có tính sai? giải quyết như nào?
Trong quá trình chuẩn hóa sử dụng dấu chấm động, giá trị mastissa sẽ được chuyển đổi bằng cách gấp đôi phần thập phân cho tới khi kết quả trở của chúng là một số nguyên, bước này có thể có những trường hợp xảy ra lặp vô hạn (giống như bạn tính toán và gặp phải trường hợp 1/3 = 0.333333 vậy 😂)

Vòng lặp vô hạn

Để giải quyết vấn đề này máy tính buộc phải giới hạn rồi làm tròn số, từ đó dẫn đến việc gặp phải sai số trong lúc làm việc với kiểu dữ liệu float. Đây thực sự là một điểm yếu bất đắc dĩ của 𝗳𝗹𝗼𝗮𝘁𝗶𝗻𝗴 𝗽𝗼𝗶𝗻𝘁 bên cạnh ưu điểm có thể biểu diễn tốt các số thực rất lớn hoặc rất nhỏ một cách thông minh. Nhưng mọi thứ đều là "trade-off" mà đúng không? cách duy nhất chúng ta có thể làm là sống chung với lũ, thông thường sẽ có các tiêu chuẩn về "ngưỡng sai số" và làm tròn được các tổ chức quy định, tuy nhiên lập trình viên cũng cần hết sức lưu ý khi so sánh giá trị đúng tuyệt đối của các số thực float.
Ví dụ minh họa việc so sánh 2 số thực - sử dụng ngưỡng sai số bằng ngôn ngữ JavaScript:
console.log(0.1 + 0.2 == 0.3); // false const toralence = 0.0001; console.log(Math.abs(0.1 + 0.2 - 0.3) < toralence); // true
Chốt lại, 𝗳𝗹𝗼𝗮𝘁𝗶𝗻𝗴 𝗽𝗼𝗶𝗻𝘁 và sai số là một phần của khoa học máy tính từ xưa đến nay và nó đã giải quyết được một bài toán rất lớn trong sự phát triển của công nghệ thông tin. Có lẽ trong tương lai gần chúng ta vẫn chưa có phương án thay thế cho cơ chế này, nhưng tương lai xa thì không nói trước được điều gì khi mà các nhà khoa học đang thử nghiệm vận hành máy tính lượng tử, với nhiều hơn hai trạng thái 1 và 0, cho tới lúc đó chúng ta vẫn cần nắm được 𝗳𝗹𝗼𝗮𝘁𝗶𝗻𝗴 𝗽𝗼𝗶𝗻𝘁 và sử dụng các số thực một cách cẩn thận nhé!
Theo dõi Techomies để xem thêm các bài viết hay trong tương lai nhé!




